| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- teachablemachine
- r
- SAS반복문
- 회귀분석실습
- 머신러닝
- SQL
- 회귀분석
- DOEND
- 본페로니
- 마케팅조사
- 모형진단
- kaggle
- Cook'sdistance
- rstandard
- format
- 캐글
- 마케터
- sasviya
- 회귀모델
- SAS
- rstudent
- infile
- 데이터청년캠퍼스
- 포지셔닝맵
- 할당문
- DIFFITS
- 데이터결합
- 마케팅
- 프로그래밍
- 마케팅공부
- Today
- Total
통수정의 성장기
R_Diagnostics in multiple linear regression_다중선형회귀 진단 본문
💡 다중선형회귀란?
: X가 여러개, 단순션형회귀와 같이 독립변수X의 변화에 따라 종속변수 Y의 변화를 선으로서 예측하는 기법→ 가정[정규성, 등분산성, 선형성, 독립성]
Diagnostics _진단
- 오차항 가정 : 정규성, 독립성, 등분산성
- 잔차 분석: 잔차의 정규성, 잔차의 독립셩, 잔차의 등분산성
rstandard vs rstudent
- rstandard : 잔차를 표준오차로 나눈 값 →internally

- rstudent : i번째 값 제외한 rstandard 값 →externally

Standard diagnostic Plots
url = '<http://www.statsci.org/data/general/hills.txt>'
races<- read.table(url,header=T, sep='\\t')
head(read.table)
#linear model
lmfit<-lm(Time~Climb+Distance, data=races)
lmfit
#diagnostic plot
par(mfrow=c(2,2))
plot(lmfit)
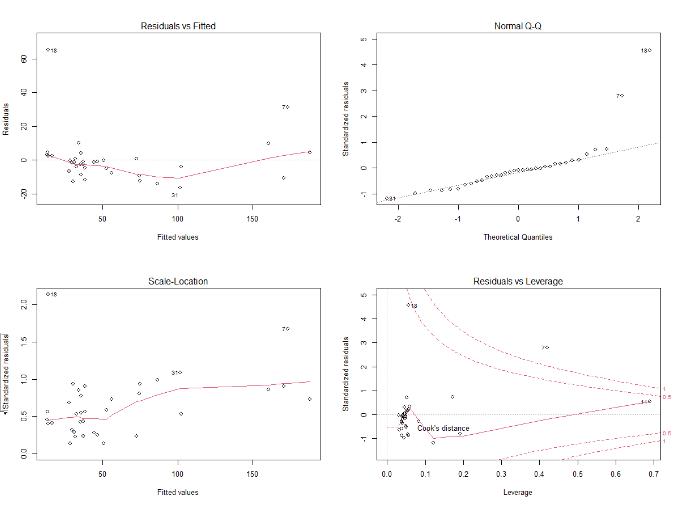
1. 정규성 검정 : 위에서 오른쪽 그래프
nomal Q-Qplot 잔차가 동일한 분산을 가진 정규성을 가지는지 확인. 선형 곡선에서 멀리 떨어져있다면 정규성에서 벗어남.
#linear model
lmfit<-lm(Time~Climb+Distance, data=races)
lmfit
par(mfrow=c(1,1))
qqnorm(rstandard(lmfit))
abline(0,1)

해당 그래프의 경우 정규성 없다고 보면 됌.
2. 등분산성 검정 : 밑에서 왼쪽 그래프
분산이 일정하면 random하게 ! 루트 rstandard VS fitted value 그래프이다.
해당 그래프는 x가 증가하며 y점이 증가하는 것으로 보임. →아마도 분산 일정xxx
3. 독립성 검정 : 위에서 왼쪽 그래프
residuals이 fitted value와 상관관계가 있냐 없냐. →Residuals VS fitted value
residual 평균이 0에 가까워야. 즉 점들이 0에 가까워야 굿.
이상값 확인 가능
4. 이상점파악 : 오른쪽 아래
leverage VS residuals
레버리지가 높고 잔차가 큰 점은 특히 영향력이 크다.
레버리지(x축) : 설명변수가 얼마나 극단에 치우쳐져 있는지
점선 밖은 outlier로 의심된다.
#이상점 바로 파악하는법
#influence.measures() : 의심 스러운 값 *로 표시됌.(한번에 summary로)
influence.measures(lmfit)<영향력있는 관측치 찾기_이상치 i는 얼마나 영향력이 큰가. >
DIFFITS
i번째 값 미포함에 따른 fitted value값의 변화량
변화가 크면 이상치인거임.
보통 1보다 크면 이상치라고 하기도 하고, 다른 값들에 비해 상대적으로 크면 그것도 이상치
#linear model
lmfit<-lm(Time~Climb+Distance, data=races)
#DFFITS-> 7,18번째 살펴봐야겠다 싶은 그래프
plot(abs(dffits(lmfit)))
abline(a=1,b=0,col="red")
#1보다 큰 이상치 값과 인덱스 불러와줌
races.table[which(abs(dffits(lmfit))>1),]
#각 점에 숫자 붙이는 법ver1
dffit<- dffits(lmfit)
text(x=1:length(dffit),y=dffit,
labels =1:length(dffit),
col="red",adj=1)
# dffit>1일때 숫자 붙여라ver2
dffit_sub<-dffit[dffit>1]
index<-which(dffit>1)
text(x=index,y=abs(dffit_sub),
labels =index,
col="red",adj=1)

Cook’s distance
i번째 삭제했을 때, 각 값이 얼마나 많이 회귀모형을 변화시키는지
#cook's distance
#그래프
plot(cooks.distance(lmfit),ylab="cook's distance")
#이상값 인덱스, 값 구하기
races.table[which(cooks.distance(lmfit)>1),]
DFBETAS
각 data 제거시 포함시의 회귀계수(b) 차이.
변수별 이상치
이상값 기준 : 다른행의 dfbeta 대비 얼마나 커야 하는가 ?
#dfbetas
dfbetas(lmfit) # 각 변수별 35개 나옴
#climb변수의 dfbetas 그래프
plot(abs(dfbetas(lmfit)[,"Climb"]))
#climb변수의 dfbeta값중 1보다 큰거
races.table[which(abs(dfbetas(lmfit)[,'Climb']) > 1),]
#distance변수의 dfbeta값중 1보다 큰거
races.table[which(abs(dfbetas(lmfit)[,'Distance']) > 1),]
Leverage(Hii) : X에서의 특이값
#linear model
lmfit<-lm(Time~Climb+Distance, data=races)
#leverage
hatvalues(lmfit)
plot(hatvalues(lmfit))
#값과 인덱스 찾기
races.table[which(hatvalues(lmfit)>0.3),]
본페로니
자료에 문제가 없어 outlier가 아님에도 유의수준이 높아 이상치로 탐지하는 경우가 있다. 더 각박한 유의수준을 줘야한다.
즉 H0 :첫번째 sample oulier이다, H0 :두번째 sample oulier이다 …100일때 여러번 검정하면서 각각의 유의수준 5%가 아닌 더 엄격해야 한다. →본페로니 하면 H1범위 아주 줄어듦.
#본페로니
n<-nrow(races)
cutoff_bonf <- qt(1-0.05/(2*n), (n-4))
races.table[which(abs(rstudent(lmfit))>cutoff),]
#본페로니 내장함수
library(car)
outlierTest(lmfit) #bonferroni pvalue 값이 더 적합(더 큼)
모형적합 후 성능평가
avPlots→ Added variable plots
crPlots→ Residual+component plots
library(car)
avPlot(lmfit,"Distance")
crPlot(lmfit,"Distance")
avPlot(lmfit,"Climb")
crPlot(lmfit,"Climb")
crPlots→ Residual+component plots
library(car)
avPlot(lmfit,"Distance")
crPlot(lmfit,"Distance")
avPlot(lmfit,"Climb")
crPlot(lmfit,"Climb")
'회귀분석' 카테고리의 다른 글
| R_Multiple linear regression_세가지 검정 (0) | 2022.06.13 |
|---|

